백준 DP 문제 풀이 (Silver) 11053번, 1932번, 1912번, 9461번 python

1. 가장 긴 증가하는 부분 수열 (11053번)

숫자 수열이 주어질 경우 가장 길게 증가하는 부분 수열의 길이를 구하는 문제입니다.

예시) {10,20,10,30,20,50} 인 경우 가장 긴 증가하는 부분 수열은 {10,20,30,50}이고 길이는 4입니다.

앞에서부터 차례로 자신을 포함하는 가장 긴 부분 수열을 구하면 됩니다.

자신을 포함한 가장 긴 수열을 구하는 방법은, 자신보다 앞에 위치하면서 자신보다 작은 숫자 중 현재 가장 긴 증가하는 부분 수열을 가지는 숫자에 자신을 붙이면 됩니다.

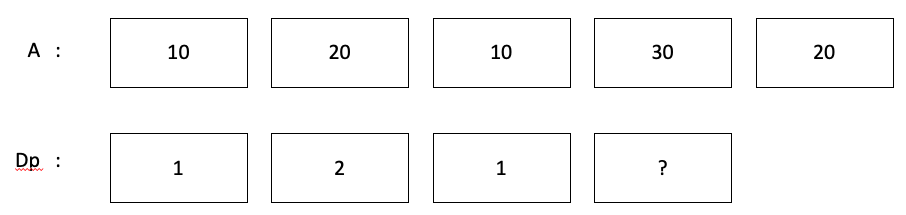
예시1

위의 예시 중 4번째 인덱스의 30을 포함한 부분 수열을 구하는 예를 들어보겠습니다.

30보다 앞에 위치한 숫자 중 30보다 작은 10,20,10 중 증가하는 부분 수열 중 가장 긴 숫자는 20입니다. 그러므로 20 다음에 30이 위치할 경우 부분 수열의 길이는 3이 되고 30을 포함했을 때 가장 긴 부분 수열의 길이는 3입니다. 이후의 숫자들도 같은 방법으로 가장 긴 부분 수열을 구해줍니다.

여기서 한 번 잘 못 제출했던 경험이 있습니다. 저는 이번 문제의 답이 dp의 마지막 원소라고 생각했습니다. 마지막에 가장 긴 부분 문자열을 가지고 있을 확률이 클 것이라 생각했기 때문입니다(사실 생각 없이 한 게 맞습니다...). 하지만, 이번 문제와 같은 경우 가장 긴 부분 수열이 어디든 위치 할 수 있기 때문에 dp 배열에서 최대값을 구해야 하는 문제였습니다.

 

 

2. 정수 삼각형 (1932번)

        7
      3   8
    8   1   0
  2   7   4   4
4   5   2   6   5

위와 같이 정수 삼각형이 주어질 경우 맨 위 7부터 시작하여 아래 층으로 이동하면서 있는 숫자를 더할 때, 선택된 숫자의 합 중 최대가 되는 경우를 구하는 문제입니다.

 

이 번 문제는 dp 배열을 어떤 식으로 해야 할지 고민이 되었습니다. 처음에 모양을 완전 이진 트리로 잘 못 파악하여 루트부터 차례로 배열로 표현하려고 했고, 이 생각을 하자마자 구조가 달라 해당 방법으로는 불가하다는 사실을 알게 되었습니다. 그래서 완전 이진 트리를 배열로 많이 표현하 듯이, 이 모양도 1차원 배열로 표현 할 수 있을 것이라고 생각했습니다. 하지만, 쉽게 떠오르지 않았고 결국 2차원 배열을 사용하는 것으로 마음을 바꿨습니다.

 

2차원 배열로 마음을 먹으니 굉장히 쉽게 해결 됐습니다. 아래 층에 위치한 숫자(A[i][j])로 내려 올 수 있는 위층의 숫자는 A[i-1][j-1], A[i-1][j] 가 된다는 것을 알게 되었고 이를 통해 문제를 해결했습니다.

위에서부터 차례로 위 층에서 내려올 수 있는 현재까지의 합 중 최대값에 자신을 더한 값을 가지고 있도록 합니다.

각 숫자는 가장자리에 위치하지 않는 이상 두 개의 숫자로 부터 내려 올 수 있으므로 두 개의 경로 중 최대값을 고르도록 하고, 가장자리에 위치할 경우 가능한 경로 하나에 대한 합을 가지고 있도록 합니다.

위에서부터 차례로 dp에 값을 채우고, dp[N-1] 배열 중 가장 큰 값이 답이 됩니다.

 

 

3. 연속합 (1912번)

n개의 수열에서 연속된 수의 합 중 최대값을 구하는 문제입니다.

연속된 숫자 중 최대값을 구하는 문제는, 이전까지 연속되었든 연속되지 않았던지 상관하지 않고 이전 숫자까지의 최대값을 포함한 경우와 포함하지 않은 경우 중 어떤 수가 더 큰지 확인하면 됩니다.

 

예시 10,-4,3,1,5,6,-35,12,21,-1 일 때,

10 다음 -4를 생각해보도록 하겠습니다. -4 이전까지 10이 최대값이므로 10을 포함할 경우는 6이고 10을 포함하지 않는다면 -4가 됩니다. 3이전까지의 연속된 최대값은 10,-4를 포함한 6이고 이를 포함한 경우는 9이고 포함하지 않는 경우는 3이됩니다. 이렇게 진행을 하면 연속된 숫자의 합 중 최대값을 구할 수 있습니다.

 

이번 문제의 답도 dp[N-1]이 아닌 max(dp)가 됩니다.

 

 

4. 파도반 수열(9461번)

이번 문제는 피보나치처럼 이전 숫자를 더해서 다음 숫자가 만들어지는 형식의 문제였습니다.

그림을 보고 바로 규칙을 떠올리기 어려웠지만, 되도록 큰 숫자들을 이용해 규칙을 찾을 수 있었습니다.

파도반 수열

dp = {1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12}입니다. 그림을 보며 찾은 규칙은

n>4일 경우 dp[n]=dp[n-1]+dp[n-5]입니다.

이를 적용하여 주어진 테스트케이스에 대한 값을 찾으면 됩니다.

 

 

 

풀이

1. 가장 긴 증가하는 부분 수열 (11053번)

N = int(input())
A = list(map(int,input().split()))

dp = [1 for _ in range(N)]

for i in range(N):
    for j in range(i):
        if A[i]>A[j]:
            dp[i]=max(dp[i],dp[j]+1)

print(max(dp))

2. 정수 삼각형 (1932번)

N=int(input())
array=[[int(input())]]
for i in range(N-1):
    array.append(list(map(int,input().split())))

dp=array[:]
for i in range(1,N):
    for j in range(i+1):
        x,y=j-1,j

        if j==0:
            dp[i][j]+=dp[i-1][j]
        elif 1<=j<i:
            dp[i][j]+=max(dp[i-1][j-1],dp[i-1][j])
        else:
            dp[i][j]+=dp[i-1][j-1]
print(max(dp[N-1]))

3. 연속합 (1912번)

N=int(input())
A=list(map(int,input().split()))
dp=[0 for _ in range(N)]
dp[0]=A[0]
answer=A[0]

for i in range(1,N):
    dp[i]=A[i]+max(dp[i-1],A[i-1])
    answer=max(answer,dp[i],A[i])

print(answer)

4. 파도반 수열(9461번)

def recursion(n):
    if dp[n]!=0:
        return dp[n]

    dp[n]=recursion(n-1)+recursion(n-5)
    return dp[n]

T=int(input())
tList=[int(input()) for _ in range(T)]
dp=[0 for _ in range(max(tList))]
dp[0]=1
dp[1]=1
dp[2]=1
dp[3]=2
dp[4]=2

for t in tList:
    print(recursion(t-1))

 

 

 

 

최근 문제가 너무 안 풀려 다시 쉬운 문제로 머리를 식히게 되었습니다. 다음 알고리즘 포스팅부터는 다시 골드 이상의 문제로 돌아오도록 하겠습니다.