백준 11437번 LCA , 11438번 LCA2

LCA란 Lowest Common Ancestor로 두 정점의 가장 가까운 공통 조상을 찾는 문제입니다

 

 

시도 1.

루트 노드인 1번 노드부터 연결된 간선을 통해 자식 노드들을 내려가게 됩니다. 이 때, 자식노드의 부모노드를 모두 저장하면서 내려가도록 합니다.

 

여기서 중요한 것은 주어지는 입력이 루트노드로부터 가까운 순이 아니므로, 모든 간선의 입력을 받은 뒤 부모노드와 자식 노드를 분간해야 된다는 것입니다.

 

모든 노드의 부모노드를 찾은 뒤, 두 정점으로부터 가까운 공통 부모를 찾아줍니다.

한 노드로부터 부모노드로 계속 이동하여 루트 노드까지 방문하고 방문한 노드에 표시를 해줍니다(visited 배열을 통해). 그 다음 다른 노드 또한 부모노드로 계속 이동하여 루트 노드까지 이동하는데 visited 배열에 표시된 노드가 나올 때까지만 이동해줍니다.

 

만약 표시된 노드가 나올 경우 해당 노드가 가장 가까운 공통 부모가 되므로 해당 노드를 출력해줍니다.

def recursion(node):
    for newNode in edges[node]:
        if not visited[newNode]:
            visited[newNode]=True
            toParent[newNode]=node
            recursion(newNode)

def visitParent(node):
    visited[node]=True
    if node==1:
        return
    visitParent(toParent[node])

for a,b in mList:
    answer=1
    visited=[False for _ in range(N+1)]
    visitParent(a)
    findCommonParent(b)
    print(answer)

하지만, 결과는 시간 초과가 나왔습니다.

 

처음에는 우선 노드의 개수가 최대 50,000이고 공통 조상을 알고 싶은 노드 쌍이 최대 10,000개가 될 수 있지만, 트리의 depth는 log(노드 개수)이기 때문에 적은 시간으로도 순회가 가능하고 그렇기 때문에 문제 없이 통과할 것이라고 생각했습니다.

하지만, 이 문제와 같은 경우 항상 완전 이진 트리의 형태를 가지지 않으므로 트리의 depth는 최악의 경우 N이 될 수 있기 때문에, 최악의 경우 트리 전체를 두 번 순회하는 경우가 발생하므로 시간 초과가 발생한 것 같습니다.

 

 

시도 2.

각 노드에 이어진 간선을 모두 저장하는 것은 기존과 동일하게 진행하고, 각 노드의 부모노드와 각 노드의 depth를 저장해줍니다.

depth와 부모 노드를 구할 경우 dfs알고리즘을 이용해줍니다.

def dfs(node, depth):
    visited[node] = True
    d[node] = depth

    for newNode in graph[node]:
        if not visited[newNode]:
            parent[newNode] = node
            dfs(newNode, depth + 1)

그 다음 가장 가까운 공통 조상을 구해줍니다.

 

우선, 두 접점의 depth가 맞을 때까지 더 깊은 위치에 있는 접점을 부모로 이동시켜줍니다.

두 접점의 depth가 동일하다면 각 노드로부터 계속 부모로 이동하면서 동일 부모가 나올 때까지 이동시켜줍니다.

def lca(a, b):
    while d[a] != d[b]:
        if d[a] > d[b]:
            a = parent[a]
        else:
            b = parent[b]

    while a != b:
        a = parent[a]
        b = parent[b]

    return a

위와 같은 경우 최악의 경우에도 한 번만 트리를 순회하고 끝나기 때문에 이전 방법과는 달리 시간 초과가 발생하지 않은 것 같습니다.

 

 

 

 

11438 LCA2

이번 문제는 이전 문제에서 시간 제한이 좀 더 줄어든 문제입니다.

시간 제한이 줄어들었기 때문에 순회에 대한 시간을 줄여주어야 합니다.

 

이전 문제에서 부모로의 이동을 한 칸씩만 했기 때문에 순회에 시간이 오래 걸리게 되었습니다.

그렇기 때문에 한 칸씩 이동하는 것이 아닌 2의 제곱 칸으로 이동 할 수 있도록 메모이제이션을 해주도록 하겠습니다.

 

parent 2차 배열은 다음과 같이 수를 저장해주도록 합니다.

예시 1

위와 같은 예시 트리가 있을 경우에 17에 대한 부모를 저장하는 방법을 다르게 해보도록 하겠습니다.

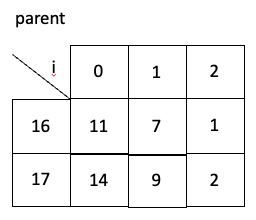
예시 2

parent배열에 저장되는 부모는 2**i 번째 부모입니다. 즉, parent[node][0]은 node의 2**0인 0 번째 부모를 뜻하게 됩니다.

그러므로 parent[17][0]은 바로 앞의 부모인 14가 되고 parent[17][1]은 1 번째 부모인 9가 됩니다.

이런식으로 모든 노드를 저장 할 경우 이동이 훨씬 빠르게 될 수 있다고 생각했습니다.

def set_parent():
    recursion(1, 0) # 1번 노드부터 depth를 구해줍니다.
    for i in range(1, DEPTH):
        for j in range(1, n + 1):
            parent[j][i] = parent[parent[j][i - 1]][i - 1]

parent[j][i]는 j노드의 2**(i-1) 노드의 i-1번째 부모입니다.

위의 17번 노드에 대해서 예시를 들어보자면 parent[17][2]는 parent[17][1]번째 노드인 9의 1 번째 부모입니다. 즉, parent[9][1]입니다.

 

lca 함수 변경

우선 두 접점의 깊이를 맞춰줍니다.

두 접점의 깊이 차이를 최대한 줄여줄 수 있는 길이를 이동 할 수 있도록(더 깊은 노드가 이동 했을 때, 덜 깊은 노드를 넘어서지 않도록), 문제에서 주어진 최대 깊이와 동일한 길이부터 0까지 내림차순으로 2**i만큼 이동 했을 때 다른 노드의 깊이보다 깊은 지역으로 이동 할 수 있는지 확인하고, 이동 할 수 있다면 이동을 해줍니다.

예시 3

위의 사진을 예시로 들면 17과 3에 대해서 같은 깊이를 찾는 경우를 살펴보겠습니다.

더 깊이 있는 17을 이동시키는데, 3의 깊이까지 가장 길게 이동 할 수 있는 거리는 2**2입니다. 그러므로 17을 우선 2로 이동 시켜줌으로써 두 노드의 깊이를 맞추어줍니다.

만약, 17과 6이라면, 6의 깊이까지 가장 길게 이동 할 수 있는 거리는 2**1이므로 17을 9로 이동 시켜준 다음, 9를 6의 깊이까지 가장 길게 이동 할 수 있는 거리인 2**0으로 이동시켜줌으로써 4로 이동하여 6과 깊이를 맞춰줍니다.

 

깊이를 맞춰 이동한 두 접점이 같은 노드를 가리킨다면 해당 노드가 LCA가 됩니다.

 

이 후 두 노드를 parent 배열을 통해 가장 먼 부모노드부터 순회하면서 같은 부모를 가리키지 않을 때에만 이동시켜줌으로써 가장 가까운 공통 조상을 찾을 수 있도록 해줍니다.

for i in range(DEPTH - 1, -1, -1):
    if parent[a][i] != parent[b][i]:
        a = parent[a][i]
        b = parent[b][i]

위와 같이 이동 할 경우 두 노드는 공통 부모 바로 아래 자식에서 순회가 멈추게 됩니다.

그러므로 한 접점의 0 번째 부모가 가장 가까운 공통 조상이 됩니다.

 

 

 

 

 

이번 문제는 순회를 더 빠르게 할 수 있는 방법에 대해 찾아보는 것이 주요했던 문제입니다. 11438번과 같은 경우 제대로 찾지 못해 풀이를 참고하면서 풀게 되어 아쉬웠습니다. 다른 분의 풀이를 참고한만큼 제대로 문제를 파악하고 다음에 한 번 더 푸는 기회를 갖는 것이 이 문제를 제대로 학습하는 방법이라고 생각됩니다.

공통 조상을 찾으면서 이동하는 것을 항상 한 칸씩 이동하는 것보다는 위의 방식과 같이 메모이제이션을 이용하면 훨씬 빠르게 찾을 수 있다는 것을 알게 되었습니다. 또한, 메모이제이션을 이용한다면 메모리의 사용량은 증가하는 대신 시간 복잡도에서 우위를 가져갈 수 있지만, 사용하지 않고 문제를 풀게 된다면 메모이제이션을 이용했을 때의 장점은 단점으로 단점은 장점으로 가져가게 될 수 있다는 것도 다시금 생각 할 수 있게 해준 문제인 것 같습니다.

 

reference : https://www.youtube.com/watch?v=O895NbxirM8&t=473s