26646번 알프스 케이블카

문제 설명

이번 문제는 여러 산맥의 정상을 다른 산의 정상으로 잇는 와이어를 설치해서 이동할 경우, 노선의 설치 비용을 최소화하는 경우를 구하는 문제입니다.

• 와이어의 설치 비용 - 와이어 길이의 제곱
• 노선의 설치 비용 - 와이어의 설치 비용의 합

알프스 케이블카

문제 풀이

아이디어

와이어 설치 비용의 최소값

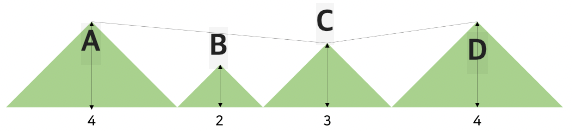
위의 사진 예시를 보도록 하겠습니다.

A-B-C를 잇는 경우와 A-C를 잇는 경우의 설치 비용을 비교해보면,

A-B-C를 잇는 경우의 설치 비용은 66

A-C를 잇는 경우의 설치 비용은 122가 됩니다.

 

위에서 확인할 수 있듯이, 산 정상을 하나라도 건너 뛰어서 와이어를 잇게 된다면 설치 비용이 커짐을 알 수 있습니다.

(모든 산은 직각 이등변 삼각형이므로 어떤 예시를 들게 되더라도, 정상 하나를 건너 뛰어서 와이어를 잇게 된다면 모든 정상을 잇는 와이어의 제곱의 합보다 크게 됩니다.)

 

증명

증명

모든 빗변을 잇는 와이어의 설치 비용

a^2 + a^2 + b^2 + b^2 + b^2 + b^2 + c^2 + c^2

= 2a^2 + 4b^2 + 2c^2

 

한 정상을 건너 뒤는 와이어의 설치 비용

(c - a)^2 + (a + 2b + c)^2

= 2a^2 + 4b^2 + 2a^2 + 4ab + 4bc

 

{모든 빗변을 잇는 와이어의 설치 비용} - {한 정상을 건너 뛰는 와이어의 설치 비용} = - (4ab + 4bc)

a>0,b>0,c>0이므로 한 정상을 건너 뛰어서 와이어를 설치했을 때의 비용이 더 많이 들게 된다.

 

그러므로, 여러 산이 있을 경우 모든 산의 정상을 이어야 최소 비용으로 와이어를 설치할 수 있게 됩니다.

 

 

풀이

위의 증명을 통해 모든 정상을 연결해야됨을 알았으므로, 모든 정상을 이어주면 됩니다.

 

 

 

해결

이번 문제는 사진 속에서는 무조건 정답을 제시해줄 것이라는 생각에 잘 못 풀 뻔 했던 문제입니다.

(문제의 사진을 맹신하지 말자...)

 

문제 링크 : https://www.acmicpc.net/problem/26646

26646번: 알프스 케이블카

코드 링크 : https://github.com/beomseok37/baekjoon/blob/master/new!/26646.py